LGS Kareköklü Sayılar Çıkmış Sorular, 2018,2019 ve 2020 yıllarında yapılan LGS sınavında çıkmış kareköklü çözümlü sorulardır. Aşağıda bulunan bağlantı ile PDF olarakta indirebilirsiniz.
LGS 2018 SORULARI

Yukarıdaki sayı doğrusunda 7 ile 10’a karşılık gelen noktaların arası 6 eş parçaya ayrılmıştır.
Buna göre A noktasına karşılık gelen sayı aşağıdakilerden hangisi olabilir?
A) √94 B) √88 C) √79 D) √68
ÇÖZÜM:
Sayı doğrusunda 7 ile 10’a karşılık gelen noktaların arası 6 eş parçaya ayrılmış.
6 eş parçanın uzunluğu = 10-7 = 3 olur.
Buradan 2 eş parçanın uzunluğu 1’dir.
7’den 1 birim gidersek A’nın yanındaki noktaya karşılık gelen sayı 8 olur. 8 = √64’e eşittir.
A sayısı √64’e çok yakın ve biraz daha büyük olduğu için seçeneklerde verilen √68 doğrudur.
Cevap D
SORU:
Altan ve Can, defterlerine kenar uzunlukları santimetre cinsinden doğal sayı olan birer kare çiziyorlar. Altan’ın çizdiği karenin alanı kenar uzunlukları 7 cm ve 9 cm olan dikdörtgenin alanından küçüktür.
Buna göre Altan ile Can’ın çizdiği karelerin alanları arasındaki fark en az kaç santimetredir.?
A) 8 B) 15 C) 32 D) 39
ÇÖZÜM:
Altan’ın çizdiği karenin alanı kenarları 7 ve 9 olan bir dikdörtgenin alanından büyük olarak verilmiş.
Dikdörtgenin alanı = 7.9 = 63 olur. 63’ten büyük en küçük tam kare 64 olduğundan karenin alanı 64’tür.
Can’ın çizdiği karenin alanı 63’ten küçük olması gerekiyor. Soruda farkın en az olması istendiği için Can’ın çizdiği karenin alanı 63’ten küçük en büyük tam kare sayı olması gerektiği için 49 olur.
İkisinin farkını alırsak 64 – 49 = 15 bulunur.
Cevap B
SORU:
Alanı 118 m² olan bir evin dikdörtgen biçimindeki odaları ve salonu dışındaki bölümlerinin toplam alanı 34 m², metrekare cinsinden bir tam kare sayıdır ve odaları alanları toplamından küçüktür.
Bu salonun kısa kenarının uzunluğu √18 m olduğunda göre uzun kenarının uzunluğu en fazla kaç metredir?
A) 7√2 B) 6√2 C) 4√2 D) 3√2
ÇÖZÜM:
Evin Alanı = 118 m2
Evin odaları ve salonu dışındaki alanı = 34 m2
118 – 34 = 84 m2 evin odaları ve salonun alanıdır.
Salonun alanı metrekare cinsinden bir tam karedir ve odaların alanları toplamından küçüktür.
Eşit olsaydılar 42 olurlardı. Bundan dolayı salonun alanı 42’den küçük olacak.
Salonun bir kenarı √18 = 3√2 olarak verilmiş. Şıklardan gideriz.
Diğer kenarı 7√2 olursa 7√2. 3√2 = 42 olur. Fakat 42’den küçük olması gerektiği için sağlamaz.
Diğer kenarı 6√2 olursa 6√2. 3√2 = 36 olur. 36 sayısı 42’den küçük ve 42’den küçük en büyük tam kare olduğu için sağlar.
Cevap B
LGS 2019 SORULARI
Şekildeki gibi bir vincin havada tuttuğu inşaat malzemesinin yerden yüksekliği √125 m ve malzemenin vincin koluna uzaklığı √45 m’dir.

Vincin kolunun yerden yüksekliği sabit kalmak üzere malzeme şekildeki konumdayken √5 m yukarı çekiliyor.
Buna göre son durumda malzemenin yerden yüksekliği, malzemenin vincin koluna uzaklığından kaç metre fazladır?
A) 2√5 B) 3√5
C) 4√5 D)5√5
ÇÖZÜM:
√125 = √(25.5) = 5√5
√45 = √(9.5) = 3√5
Vincin kolunun yerden yüksekliği sabit kalmak üzere malzeme şekildeki konumdayken √5 m yukarı çekiliyor. Bu durumda
Vince √5 m yaklaştığı için o mesafeden √5 m çıkarırız, yerden yüksekliğine √5 ekleriz.
3√5 – √5 = 2√5 m olur.
5√5 + √5 = 6√5 m olur.
6√5 – 2√5 = (6-2) √5 = 4√5 m olur.
Cevap C

ÇÖZÜM:
Elde edilen kare şeklindeki kağıdın alanı 27 olarak verilmiş ve dikdörtgen şeklindeki kağıdın alanının 3 katı olduğundan, dikdörtgen şeklindeki kağıdın alanı 9 dur.
Karenin bir kenarı ile Dikdörtgenin uzun kenarının eşit olduğunu şekilden görebiliyoruz.
Karenin bir kenarına a diyelim.
a2 = 27 ise a = √27
a = 3√3 olur.
Dikdörtgenin kısa kenarına x diyelim.
Dikdörtgenin alanı kısa kenar çarpı uzun kenar olduğundan
9 = x .3√3 ise x= √3 bulunur.
Burada 3√3 ne ile çarparsak 9’u elde edebiliriz diye düşünebiliriz.
Cevap D
LGS 2020 SORULARI

ÇÖZÜM:
Bilgi: Başlangıç çizgisinden atış yapan bir oyuncunun attığı bilye, parkurda gösterilen mavi bölgede kalmış.
Mavi bölgenin 6 ile 7 arasında olduğu şekilde verilmiş. Bilye mavi bölgede olduğu için bize sormak istediği şıklardan hangisi 6 ile 7 arasında değildir.
Kıyaslama yapabilmek için tüm verilen sayıları kök içinde yazmamız gerekiyor.
6 = √36, 7 = √49 olduğundan seçeneklerde bu aralıkta olmayanı bulacağız.
2√10 = √(4.10) = √40
3√5 = √(9.5) = √45
4√3 = √(16.3) = √48
2√13 = √(4.13) = √52
√52 sayısı √36 ile √49 arasında değildir.
Cevap D

ÇÖZÜM:
Bilgi: Aynı hat üzerinde bulunan ardışık iki istasyon arasındaki mesafeler birbirine eşittir.
NOT: Trenlerin gittiği yolların uzunluklarını kıyaslayacağımız için D noktasından S’ye kadar olan kısmı 3 trende gittiği için uzunluğa dahil etmeyeceğiz.
K treni ardışık iki istasyon arası √2 olan 15 tane gittiği için toplamda
15.√2 = 15√2 = √450 km gitmiştir
L treni ardışık iki istasyon arası √5 olan 8 tane gittiği için toplamda
8.√5 =8√5 = √320 km gitmiştir.
M treni ardışık iki istasyon arası √3 olan 8 tane gittiği için toplamda
13.√3 = 13√3 = √507 km gitmiştir.
√507 > √450 > √320 olduğundan M > K > L olur.
Cevap D
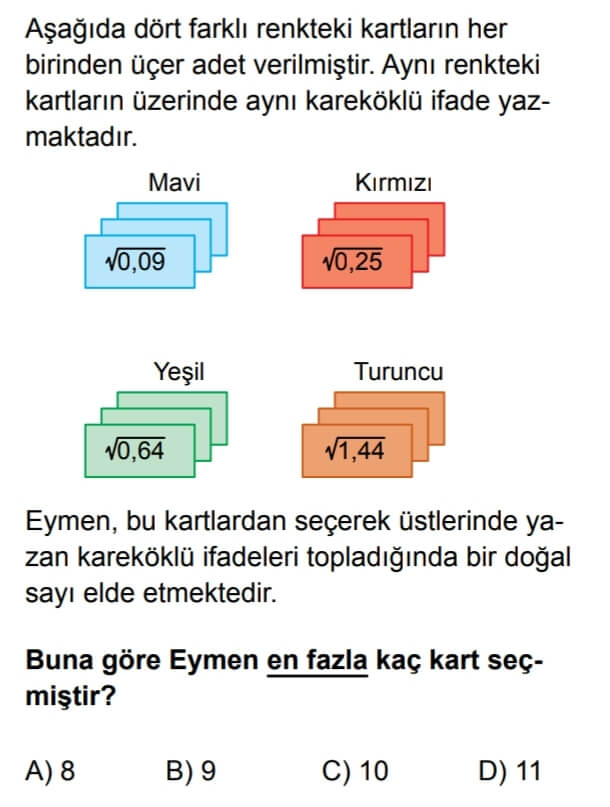
ÇÖZÜM:
Bilgi: Dört farklı renkteki kartların her birinden üçer adet verilmiştir. Aynı renkteki kartların üzerinde aynı kareköklü ifade yazmaktadır.
√(0,09) = 0,3 = 3/10
√(0,25) = 0,5 = 5/10
√(0,64) = 0,8 = 8/10
√(1,44) = 1,2 = 12/10
Topladığında doğal sayı elde edecek, en fazla kartı seçmesi için küçük olanları toplamalıyız.
3.(0,3) + 3.(0,5) +3.(0,8) = 4,8 olur. Burada turuncu kartların değeri büyük olduğu için sona sakladık. Toplamın doğal sayı olabilmesi için bir tane turuncu kartı ekleriz.
4,8 + 1,2 = 6 doğal sayı elde ederiz.
Toplamda 3+3+3+1 = 10 tane kart seçtik.
Cevap C

ÇÖZÜM:
Bilgi: Alanları santimetrekare cinsinden 10’dan büyük birer tam kare pozitif tam sayıya eşit olan karesel bölgelere ayrılmış.
En az sorulduğu için alanları küçük olacak şekilde kenarları alırız.
A karesinin bir kenarı 4 olarak alabiliriz alanı 16 olur ve 10’dan büyük ilk tam karedir.
C karesinin bir kenarı 2 tane A’ya eşit olduğu için C’nin bir kenarı 4+4 = 8’dir. Alanı = 64 olur.
A’nın bir kenarı ile C’nin bir kenarı B’nin 2 tane kenarına eşit olduğu için 4+8 = 2B ise B = 6 olur. B’nin bir kenarı 6’dır. Alanı = 36 olur.
D karesinin bir kenarı B ile C’nin bir kenarının toplamına eşit olduğundan D = 6+8 = 14’dür. Alanı = 196 olur.
Dikdörtgenin Alanı = 2A + 2B + C + D
Dikdörtgenin Alanı = 2.16 + 2.36 + 64 + 196
Dikdörtgenin Alanı = 364 bulunur.
Cevap C
SORU:
Alanı 1050 cm2 olan bir kare şeklindeki bir panoya kenarlarından birinin uzunluğu 5’in tam sayı kuvveti, diğerinin uzunluğu 2’nin tam sayı kuvveti olan dikdörtgen şeklindeki bir afiş, pano yüzeyinden taşmayacak şekilde asılacaktır.
Buna göre afişin bir yüzünün alanı en fazla kaç santimetrekaredir?
A) 1000 B) 800 C) 640 D ) 400
ÇÖZÜM:
Alanı 1050 cm2 olan bir kare verilmiş. Bir kenarı √1050‘dir. √1050‘nin hangi iki tam sayı arasında olduğunu bulalım.
√1024 < √1050 √ < 1089 olduğundan 32 < √1050 < 33 arasındadır.
Karenin içine bir pano asılacak. Asılacak olan panonun bir kenarı √1050’den yani 32,5 (örneğin) gibi bir sayıdan küçük olması gerekiyor.
Asılacak panonun bir kenarı 2’nin kuvveti diğer kenarı 5’in kuvveti olacak. Ayrıca alanı en büyük olması istendiği için bir kenarı 25 = 32,
Diğer kenar 52 = 25 olabilir.
Buradan panonun alanı = 32.25 = 800 cm2 bulunur.
Cevap B
- 8.Sınıf Çarpanlar ve Katlar Yeni Nesil Sorular Çözümlü
- 8.Sınıf Üslü Sayılar Yeni Nesil Sorular Çözümlü
- 8. Sınıf Kareköklü Sayılar Yeni Nesil Sorular 1 Çözümlü
- 8. Sınıf Kareköklü Sayılar Yeni Nesil Sorular 2 Çözümlü
- Veri Analizi Yeni Nesil Sorular Çözümlü
- Olasılık Yeni Nesil Sorular Çözümlü
- 8. Sınıf Cebirsel İfadeler ve Özdeşlikler Yeni Nesil Sorular Çözümlü
